Yksinkertainen säästölaskin
Yksinkertaisen säästölaskurin avulla voidaan laskea maturiteetti, jonka on oltava yksilön käytettävissä, johon hänellä on mahdollisuus sijoittaa, ja hän valitsee, missä voi maksimoida tuottonsa.
Yksinkertainen säästölaskin
M = I * (1 + r) n * F + i * ((1 + r) n * F - 1) / r
Jossa,- I on alkuinvestoitu summa.
- r on korko.
- n on jaksojen lukumäärä, joille yksinkertaisia säästöjä tehdään.
- F on koron maksamisen tiheys
- i on säännöllisin väliajoin sijoitettu kiinteä summa.
Tietoja yksinkertaisesta säästölaskimesta
Kaava on seuraavanlainen:
Matemaattisesti se voidaan laskea kertaluonteisille yksinkertaisille säästöille:
M = I * (1 + r / F) n * FToiseksi, jos tehdään kuukausittain yksinkertaisia säästöjä, laskelma:
M = I * (1 + r) n * F + i * ((1 + r) n * F - 1 / r)Jossa,
- M on kokonaissumma yksinkertaisen säästökauden lopussa
- I on alkuinvestoitu summa
- i on säännöllisin väliajoin sijoitettu kiinteä summa
- r on korko
- F on koron maksamisen tiheys
- n on jaksojen lukumäärä, joille yksinkertaisia säästöjä tehdään.
Monet pankit ja muut rahoituslaitokset kilpailevat markkinoilla houkutellakseen talletuksia voidakseen tehdä enemmän liiketoimintaa, eli lainata rahaa yrityksille tai korkean nettovarallisuuden omaaville henkilöille. Jotkut pankit maksavat korkeamman koron, jos talletukset ylittävät tietyt kynnysrajat ja pidetään tilillä, tai muuten he maksavat vakiokorkoa. Lisäksi koronmaksutaajuuksissa voi olla ero; esimerkiksi korkoa voitaisiin lisätä ja maksaa neljännesvuosittain, puolivuosittain tai vuosittain pankista riippuen. Siksi tällä laskimella yksilöt pystyisivät määrittämään, minkä rahoituslaitoksen tulisi valita sijoittavansa rahansa vertaamalla pääomalainojensa maturiteettia tai tuottoa.
Kuinka laskea yksinkertaiset säästöt?
Seuraavat vaiheet on noudatettava yksinkertaisten säästöjen laskemiseksi.
Vaihe # 1 - Määritä, mikä summa sijoitetaan, onko se lumpumissa vai onko myös määräajoin sijoittamista, niin sama tulisi ottaa huomioon säästökoron laskennassa.
Vaihe # 2 - Selvitä korkoprosentti, joka on käytettävissä yksilön optioissa ja joka ansaitaan tai jonka odotetaan ansaittavan yksinkertaisista säästöistä.
Vaihe # 3 - Määritä nyt ajanjakso, jolle se investoidaan, ja useimmiten ne ovat pitkällä aikavälillä ja riippuvat tapauskohtaisesti.
Vaihe # 4 - Jaa korko korkojen tai yksinkertaisten säästöjen korkojen maksamisjaksojen lukumäärällä. Esimerkiksi jos maksettu korko on 5% ja se maksaa kuukausittain, korko olisi 5% / 12, mikä on 0,416%.
Vaihe # 5 - Käytä nyt kaavaa, josta keskusteltiin edellä kohdassa 1), jos yksinkertaisista säästöistä tehdään kertasuosituksia, ja käytä kaavaa 2), jos yksinkertaisten säästöjen määrä tehdään säännöllisin väliajoin yhdessä kaikkien käytettävissä olevien vaihtoehtojen alkuarvojen kanssa .
Vaihe # 6 - Tuloksena oleva luku on maturiteettimäärä, joka sisältäisi myös yksinkertaiset säästötulot ja valitsi sen, jolla on korkein koronmaksu.
Esimerkki yksinkertaisista säästölaskureista
Herra William on nyt aikuinen ja on innoissaan avaamaan ensimmäisen säästötilisi. Hän on etsinyt rahoituslaitosta, joka tarjoaa korkoja, mutta on hämmentynyt, koska hän ei saa sitä, mikä pankki tuottaa hänelle korkeimman tuoton. Alla on lainauksia, jotka herra William on valinnut.

Hän haluaa sijoittaa 1500 dollaria jommallekummalle tilille, ja sijoittaa tavan, jolla tili maksaa korkoa. Esimerkiksi, jos pankki maksaa puolivuosittain, summa sijoitetaan tasaisesti kunkin jakson lopussa ja jatkaa niin 10 vuoden ajan.
Annettujen tietojen perusteella sinun on laskettava summa, jonka hän säästää, ja korot, jotka hän ansaitsee, ja mihin pankkiin hänen tulisi sijoittaa.
Ratkaisu:
Meille annetaan seuraavat yksityiskohdat:
PANKKI I
- I = Alkuperäinen määrä on nolla
- r = korko, joka on 3,00%, ja neljännesvuosittain se on 3,00% / 4, joka on 0,75%
- N = taajuus, joka on tässä neljännesvuosittain; siten se on 4
- n = yksinkertaisten säästöjen vuosimäärä, joka tässä on 10 vuotta.
- i = Se on säännöllinen sijoitettava summa, joka on 1500/4, joka on 375 dollaria

Nyt voimme käyttää alla olevaa kaavaa laskeaksesi maturiteetin määrän.
M = I * (1 + r) n * F + i * ((1 + r) n * F - 1) / r
- = 0 * (1 + 0,75%) 10 * 4 + 375 * ((1 + 0,75%) 10 * 4-1 / 0,75%)
- = 17,417,43
Maturiteetti on 17 417,43
Ansaittu korko olisi 17 417,43 dollaria - 375 * 40 dollaria = 2417,43 dollaria.

PANKKI II
- I = Alkuperäinen määrä on nolla
- r = korko, joka on 3,12%, ja puolivuosittain se on 3,12% / 2, mikä on 1,56%.
- N = taajuus, joka on täällä puolivuosittain, joten se on 2
- n = yksinkertaisten säästöjen vuosimäärä, joka tässä on 10 vuotta.
- i = Se on säännöllinen sijoitettava summa, joka on 1500/2 eli 750 dollaria

Nyt voimme käyttää alla olevaa kaavaa laskeaksesi maturiteetin määrän.
M = I * (1 + r) n * F + i * ((1 + r) n * F - 1 / r)
- = 0 * (1 + 1,56%) 10 * 2 + 750 * ((1 + 1,56%) 10 * 2-1) / 1,56%
- = 17 445,58 dollaria
Maturiteetti on 17 445,58 dollaria
Ansaittu korko olisi 17445,58 dollaria - (750 dollaria * 20) = 2445,58 dollaria.

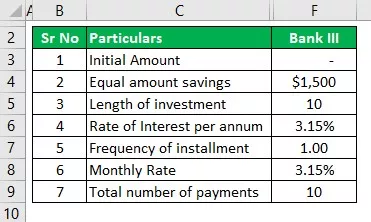
PANKKI III
- I = Alkuperäinen määrä on nolla
- r = korko, joka on 3,15%, ja vuosittain se on 3,15% / 1, mikä on 3,15%
- N = Taajuus, joka on täällä vuosittain, joten se on 1
- n = yksinkertaisten säästöjen vuosimäärä, joka tässä on 10 vuotta.
- i = Se on säännöllinen sijoitettava summa, joka on 1500/1, joka on 1500 dollaria
Nyt voimme käyttää alla olevaa kaavaa laskeaksesi maturiteetin määrän.
M = I * (1 + r) n * F + i * ((1 + r) n * F - 1) / r
- = 0 * (1 + 3,15%) 10 * 1 + 1500 * ((1 + 3,15%) 10 * 1 - 1) / 3,15%
- = 17 315,08 dollaria
Maturiteetti on 17 315,08 dollaria
Ansaittu korko olisi 17315,08 dollaria - (1500 dollaria * 10) = 2315,08 dollaria.

Suurin ansaittu summa on pankissa II, joten hänen pitäisi avata tili Pankki II: ssa.

Johtopäätös
Tätä laskinta, kuten edellä on käsitelty, voidaan käyttää vertailemaan eri maturiteettimääriä rahoituslaitoksessa, koska korkeampi korko ei takaa suurinta absoluuttista määrää, kuten yllä olevassa esimerkissä nähdään. Siksi pitäisi laskea ja verrata maturiteettisummia ja tehdä sitten päätös.








