Mikä on korrelaatiokerroin?
Korrelaatiokerrointa käytetään määrittämään, kuinka vahva on suhde kahden muuttujan välillä ja sen arvot voivat vaihdella välillä -1,0 - 1,0, missä -1,0 edustaa negatiivista korrelaatiota ja +1,0 edustaa positiivista suhdetta. Se ottaa huomioon muuttujien suhteelliset liikkeet ja määrittelee sitten, onko niiden välillä mitään yhteyttä.
Korrelaatiokertoimen kaava
r = n (∑xy) - ∑x ∑y / √ (n * (∑x 2 - (∑x) 2 )) * (n * (∑y 2 - (∑y) 2 ))
Missä
- r = korrelaatiokerroin
- n = havaintojen lukumäärä
- x = 1 s muuttuja yhteydessä
- y = 2. muuttuja
Selitys
Jos kahden muuttujan välillä on korrelaatio tai sanoa suhde, sen on osoitettava, jos joku muuttuja muuttuu arvossa, niin myös toinen muuttuja pyrkii muuttumaan arvossaan, esimerkiksi erityisenä, joka voi olla joko samassa tai päinvastaiseen suuntaan. Yhtälön osoittaja suorittaa testin ja yhdessä liikkuvien muuttujien suhteellisen voimakkuuden, ja yhtälön nimittäjäosa skaalaa osoittajan kertomalla muuttujien erot neliönmuuttujista.
Esimerkkejä
Esimerkki 1
Harkitse seuraavia kahta muuttujaa, x ja y, sinun on laskettava korrelaatiokerroin.
Alla on annettu laskentatiedot.

Ratkaisu:
Edellä olevaa yhtälöä käyttämällä voimme laskea seuraavan

Meillä on kaikki edellisen taulukon arvot n = 4.
Syötetään nyt arvot korrelaatiokertoimen laskemiseksi.

Siksi laskelma on seuraava,

r = (4 * 25 032,24) - (262,55 * 317,31) / √ ((4 * 20 855,74) - (262,55) 2 ) * ((4 * 30 058,55) - (317,31) 2 )
r = 16 820,21 / 16 831,57
Kerroin on -

Kerroin = 0,99932640
Esimerkki 2
Maa X on kasvava talousmaa, ja se haluaa tehdä riippumattoman analyysin keskuspankin päätöksistä korkomuutoksista riippumatta siitä, ovatko ne vaikuttaneet inflaatioon ja onko keskuspankilla mahdollisuus hallita sitä.
Seuraavassa esitetään yhteenveto korkotasosta ja maassa keskimäärin noina vuosina vallinneesta inflaatioasteesta.
Alla on annettu laskentatiedot.

Maan presidentti on pyytänyt teitä tekemään analyysin ja pitämään siitä esityksen seuraavassa kokouksessa. Käytä korrelaatiota ja määritä, onko keskuspankki saavuttanut tavoitteensa vai ei.
Ratkaisu:
Edellä esitetyn kaavan avulla voimme laskea korrelaatiokertoimen. Käsitellään korkoa yhtenä muuttujana, esimerkiksi x, ja inflaatioastetta toisena muuttujana y: nä.

Meillä on kaikki edellisen taulukon arvot n = 6.
Syötetään nyt arvot korrelaatiokertoimen laskemiseksi.


r = (6 * 170,91) - (46,35 * 22,24) / √ ((6 * 361,19) - (46,35) 2 ) * ((6 * 82,74) - (22,24) 2 )
r = -5,36 / 5,88
Korrelaatio on -

Korrelaatio = -0,92
Analyysi: Vaikuttaa siltä, että koron ja inflaation välinen korrelaatio on negatiivinen, mikä näyttää olevan oikea suhde. Korkotason noustessa inflaatio laskee, mikä tarkoittaa, että niillä on taipumus liikkua vastakkaiseen suuntaan toisistaan, ja yllä olevasta tuloksesta käy ilmi, että keskuspankki onnistui panemaan korkopolitiikkaa koskevan päätöksen täytäntöön.
Esimerkki 3
ABC-laboratorio tutkii pituutta ja ikää ja halusi tietää, onko niiden välillä mitään yhteyttä. He ovat keränneet 1000 ihmisen otoksen kullekin luokalle ja keksineet keskimääräisen korkeuden tässä ryhmässä.
Alla on annettu tietoja korrelaatiokertoimen laskemiseksi.

Sinun on laskettava korrelaatiokerroin ja tehtävä johtopäätös, että jos mitään yhteyttä on olemassa.
Ratkaisu:
Iän käsitteleminen yhtenä muuttujana, sanokaa x, ja korkeuden (senttimetreinä) käsitteleminen toisena muuttujana y: nä.

Meillä on kaikki edellisen taulukon arvot n = 6.
Syötetään nyt arvot korrelaatiokertoimen laskemiseksi.

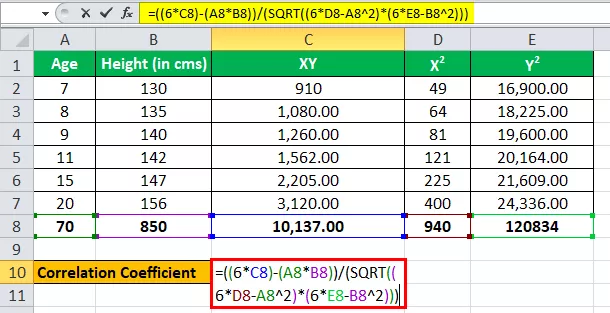
r = (6 * 10 137) - (70 * 850) / √ ((6 * 940 - (70) 2 ) * ((6 * 1,20834) - (850) 2 )
r = 1 322,00 / 1361,23
Korrelaatio on -

Korrelaatio = 0,971177099
Osuvuus ja käyttö
Sitä käytetään tilastoissa pääasiassa tarkasteltavien muuttujien välisen suhteen vahvuuden analysointiin ja lisäksi mitataan myös, onko annettujen tietojoukkojen välillä lineaarinen suhde ja kuinka hyvin ne voisivat olla yhteydessä toisiinsa. Yksi yhteyksistä, joita käytetään korrelaatiossa, on Pearsonin korrelaatiokerroin.
Jos muuttujan arvon muutos ja kyseisen muuttujan muutos yhdessä arvon kanssa, tämän suhteen ymmärtäminen on kriittistä, koska edellisen muuttujan arvoa voidaan käyttää ennustamaan jälkimmäisen muuttujan arvon muutos. Korrelaatiolla on tänä modernina aikakautena monta eri käyttötapaa, kuten sitä käytetään finanssialalla, tieteellisessä tutkimuksessa ja missä ei. Mutta on kuitenkin tärkeää tietää, että korrelaatiolla on kolme päätyyppistä suhdetta. Ensimmäinen on positiivinen suhde, joka ilmoittaa, että jos muuttujan arvossa tapahtuu muutos, siihen liittyvässä muuttujassa tapahtuu muutos samaan suuntaan. Vastaavasti, jos negatiivinen suhde on olemassa, siihen liittyvä muuttuja käyttäytyy vastakkaiseen suuntaan. Jos korrelaatiota ei ole, r tarkoittaa nolla-arvoa.Katso alla olevat kuvat käsitteen ymmärtämiseksi paremmin.









